Aufgabe:
Bestimmen Sie den Wert des Integrals für den angegeben Integrationsbereich.
Skizzieren Sie dazu zuerst den Integrationsbereich G. Verwenden Sie auch Polarkoordinaten.
\( \int \limits_{G}\left(x^{2}+y^{2}\right) d(x, y) \quad G=\left\{(x, y) \in \mathbb{R}^{2}:|x| \geq 1 \text { oder }|y| \geq \frac{1}{2}, x^{2}+y^{2} \leq 4\right\} \)
Problem/Ansatz:
Text erkannt:
\( \int x \)
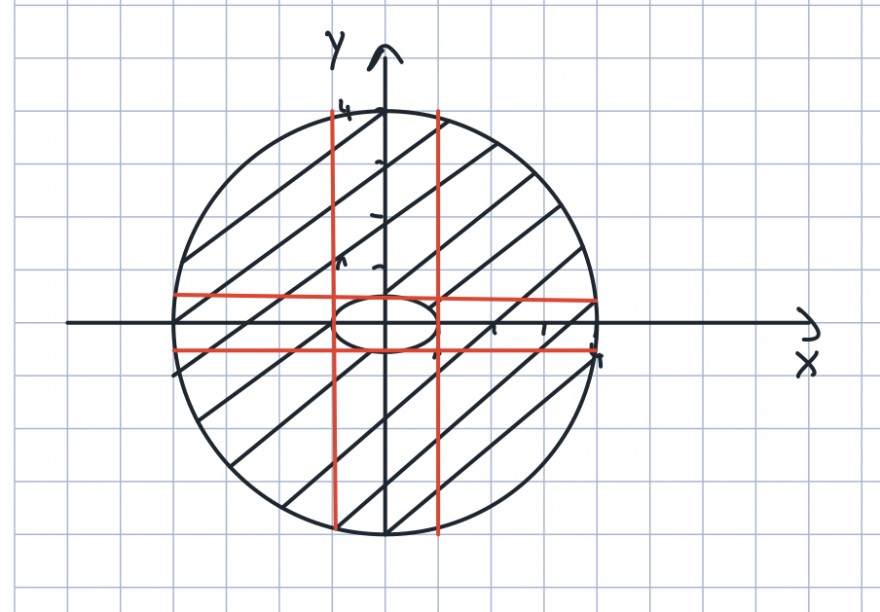
Hallo, die Skizze habe ich bereits versucht anzufertigen, allerdings bin ich mir bei der Mengen Bezeichnung nicht sicher, wie ich das oder einbette. Meine Idee war jetzt, das mittlere, von den roten Linien erzeugte Rechteck von der Kreisscheibe abzuziehen.
Die weiteren Schritte sind mir allerdings nicht ganz klar. Mein Ansatz hier für die Polarkoordinaten:
φ [0,2π] , r konnte ich noch nicht festlegen
Vielen Dank schonmal vorne weg für die Hilfe