Aufgabe:
Konvergenz foldengen Reihe bestimmen
Problem/Ansatz:
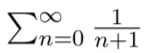
Text erkannt:
\( \sum \limits_{n=0}^{\infty} \frac{1}{n+1} \)
Wenn man da das Quotientenkriterium anwendet, bekommt man (n+1)/(n+2)=unendlich/unendlich - Anwendung von L Hospital - Grenzwert wäre ja 1.
Die Reihe soll aber konvergieren.
Wieso ist meine Überlegung falsch? Mir ist klar, dass es sich um eine harmonische Reihe haldelt, aber was ist an meiner Überlegung falsch?
Danke.