Das ist eine ziemlich fummelige Arbeit. Ich würde erstmal alle Punkte abbilden und dann schauen wie der Schatten fällt, zusammengesetzt werden muß:
Von einem Bildpunkt (b1,b2,b3) mit v auf Boden z=0 und Wand x=0.
p:={b1,b2,b3} + t {v1,v2,v3}
z(p)=0: ===> {t = -b3/v3}
t∈p ===> \(P_z:=\left(\begin{array}{r}-b3 \cdot \frac{v1}{v3} + b1\\-b3 \cdot \frac{v2}{v3} + b2\\0\\\end{array}\right)\)
PZ:\(\left(\begin{array}{rrr}1&0&\frac{-v1}{v3}\\0&1&\frac{-v2}{v3}\\0&0&0\\\end{array}\right)\)
PZ {A,B,C,D,E,F,G,H,S}
das gleiche mit x(p)=0
PX:\(\left(\begin{array}{rrr}0&0&0\\\frac{3}{5}&1&0\\\frac{-3}{5}&0&1\\\end{array}\right)\)
PX {A,B,C,D,E,F,G,H,S}
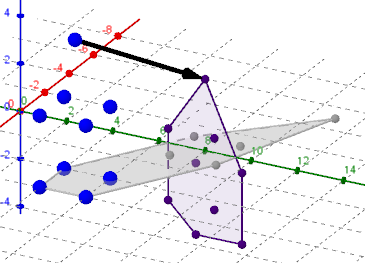
ggf: https://www.geogebra.org/m/cvmyzugu