Wie groß ist die Wahrscheinlichkeit, dass sich dabei kein nicht verwendbarer Zylinder befindet?

Question

Aufgabe:

Zum Bau von Verbrennungsmotoren wird ein Posten von 500 Zylindern geliefert. Es ist bekannt, dass 2% aller produzierten Zylinder einen Durchmesser haben, der außerhalb der Toleranzgrenzen liegt, also für diese Motoren nicht verwendet werden können. Es werden 50 Zylinder überprüft. Wie groß ist die Wahrscheinlichkeit, dass sich dabei kein nicht verwendbarer Zylinder befindet?

Problem/Ansatz:

Hier muss ich die hypogeometrische verteilung verwenden. Aber da steht was mit prozent. Wie könnte man das lösen?

Answer 1

Hier muss ich die hypogeometrische verteilung verwenden

Nein, weil die genaue Anzaht der fehlerhaften Z. in den 500 unbekannt ist.

p= (1-0,02)^50 = 36,42%

Answer 2

Hallo!

So weit ich das noch weis(Januar schwerer Arbeitsunfall) Kommt das auf die Größe der Grundgesamtheit an. Dann geht es um den sogenannten Losumfang, hier also 500 Stück pro Lieferung. Nun kommen wir zu den Prüfniveaus:

S1, S2, S3

Dann noch römisch I II und III.

Ferner wird dann der sogenannte AQL, also der akzeptierbare Qualitätslevel festgelegt. Schön brav auf englisch.

Geht übrigens nach Schädelbruch nicht mehr. Frühestens 2099, bin dann aber 134 Jahre alt...........

Das sind 0,04

0,065

0,1

0,15

0,24

1

1,5

2,4

4

6,5 und dann 25

Das sind Prozent pro hundert Teile. Da hängt aber ab, wie viele Teile dann Hops gegangen sind.

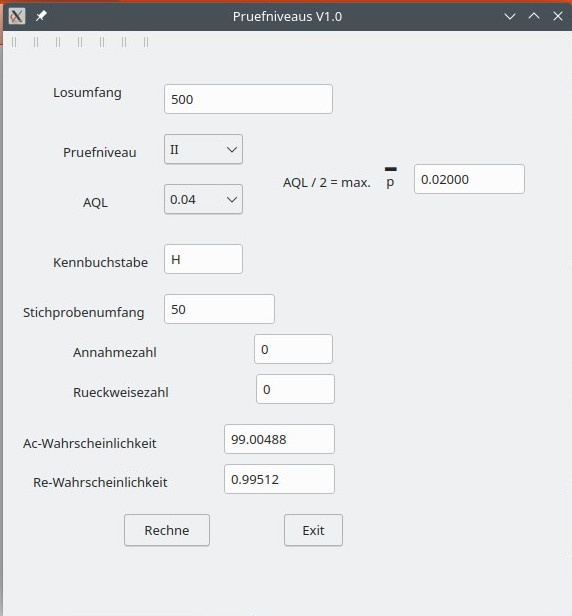
Bei einen Stichprobenumfang von 50 Teilen und AQL 0,04 sind das etwa 2 Prozent miese Teile. Da ja höchstens die Hälfte der AQL dann Ausschuss sein sollte. Der Kennbuchstabe laut DGQ(Deutsche Gesellschaft für Qualität) wäre hier H.

ÄHättest du hier AQL 0,1 dann wäre hier eine Annahmezahl von 0 Ausschuss und eine Rückweisezahl von 1.

Software für Linux und Libreoffice findest du bei libreoffice-forum.de

Geh dann auf Infos bei der Hauptseite. Da findest du viel Tabellenkalkulation für so was. Habs vor etwa 8 Jahren geschrieben.

Was für QT kompilierbare c++ Software gibt es auch irgendwo. Kann es aber nicht mehr sagen wo, da Dachschädelbruch mit 1,5 cm Gehirnversatz und eine Menge anderes Zeugs. Ich hoffe du kannst da was brauchen. Das QT ist auch bis auf die Daten auf meinen Mist in c++ gewachsen..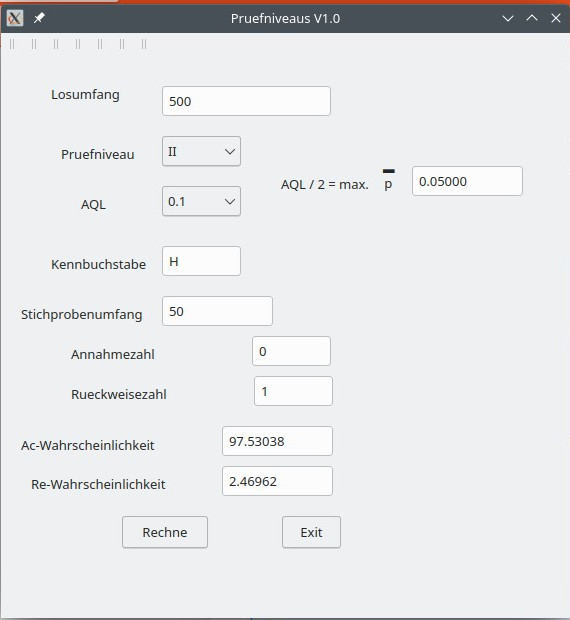

Text erkannt:

Pruefniveaus V1.0
Losumfang
\( 500 \)
Pruefniveau
\( \mathrm{AQL} / 2=\max . \overline{\mathrm{p}} 0.05000 \)
Kennbuchstabe
Stichprobenumfang
50
Annahmezahl
0
Rueckweisezahl
1
Ac-Wahrscheinlichkeit
\( 97.53038 \)
Re-Wahrscheinlichkeit
\( 2.46962 \)
Rechne
Exit

Das wäre in der Grafik die Sache mit AQL 0,1

Hier mit AQL 0,04

Text erkannt:

Losumfang
\( 500 \)
Pruefniveaus \( \mathrm{V} 1.0 \)
Pruefniveau
\( \mathrm{AQL} / 2=\max . \overline{\mathrm{p}} 0.02000 \)
AQL
\( 0.04 \)
Kennbuchstabe
Stichprobenumfang
50
Annahmezahl
0
Rueckweisezahl
0
Ac-Wahrscheinlichkeit
\( 99.00488 \)
Re-Wahrscheinlichkeit
\( 0.99512 \)
Rechne
Exit

Da dürfte also nichts schief gehen.