Mehrdimensionale Nullstellen bestimmen im Diagramm

Question

Hallo,

ich habe eine Aufgabe, die ich nicht ganz verstehe:

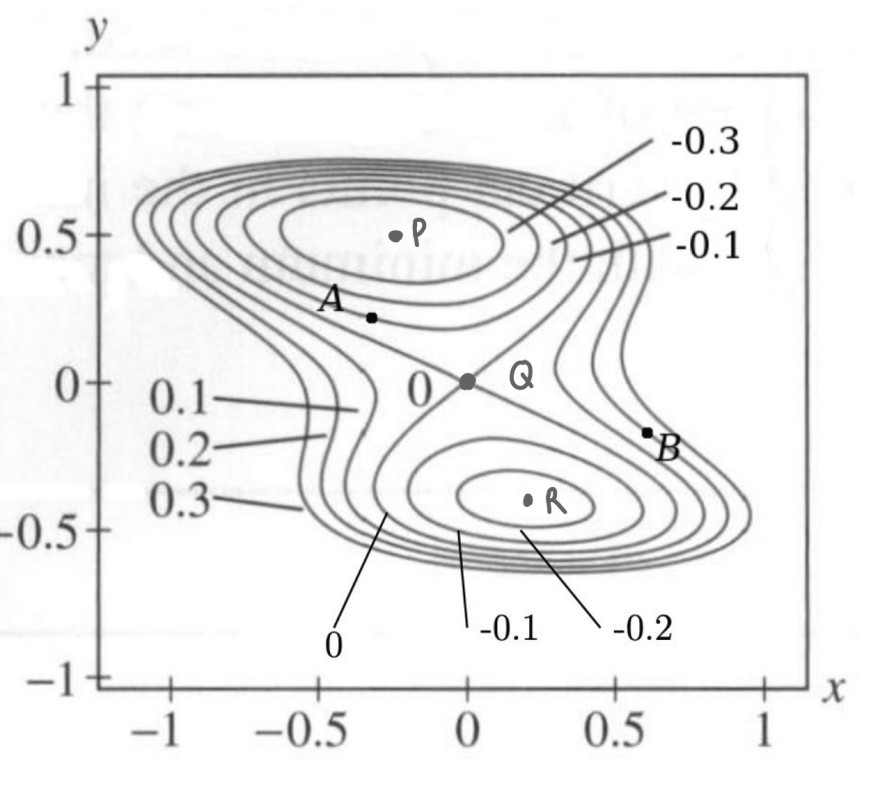
Gezeigt ist ein Konturdiagramm einer Funktion f ∈ C²(IR², IR).

i.Zeichne ∇f bei A und B ein

ii.Markiere die drei Punkte (P,Q,R), an denen ∇f = 0 sind

iii.Welche der Punkte P, Q, R sind: lokale Maxima? Lokale Minima? Sattelpunkte? (Ohne Begründung)

Ich habe unten das Bild dazu hochhgeladen und die Punkte markiert. Ich vermute P = lokale Maxima, Q = Sattelpunkt und R = lokale Minima. Korrigiert mich gerne, falls es nicht stimmt! zur i. haben ich noch nichts

Vielen Dank für die Hilfe!

Answer 1

Bei P ist kein Maximum.

Der Gradient von f an einem Punkt X steht senkrecht auf der Konturlinie durch X und zeigt in die Richtung des Anstiegs.

Comments

Ist dann P Minima und R Maxima? Muss ich für die i. einfach eine "Linie" von Punkt A bzw. Punkt B Richtung Anstieg zeichnen?

---

Wenn das Höhenlinien sind, dann geht es zu R und P "runter"....

---

Also beide Minima? Oder verstehe ich Ihre Antwort falsch